Différences entre les versions de « Logique combinatoire par liens »
(→Astuce) |
|||
| (83 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{sommaire|niveau= | {{sommaire|niveau=1|flottant=left}} | ||
=='''Introduction'''== | =='''Introduction'''== | ||
{{Infobox IPX800 | {{Infobox IPX800 | ||
| titre = Logique combinatoire | | titre = Logique combinatoire | ||
| image = | | image =logique_links_v5.jpg | ||
| famille = IPX800 V5 | | famille = IPX800 V5 | ||
| date-create = 22/10/2023 | | date-create = 22/10/2023 | ||
| date-update = | | date-update = 28/10/2023 | ||
| auteur = @fgtoul | | auteur = @fgtoul | ||
}} | |||
Le moteur de scénario de l'ipx800 V5 permet de créer des combinaisons logiques grâce aux opérateurs ET, OU, | |||
Le moteur de scénario de l'ipx800 V5 permet de créer des combinaisons logiques grâce aux opérateurs ET, OU, NON. | |||
Nous pouvons tout à fait créer ce même type de condition complexe en utilisant des liens seulement. | Nous pouvons tout à fait créer ce même type de condition complexe en utilisant des liens seulement. | ||
| Ligne 16 : | Ligne 18 : | ||
L’astuce consiste à transformer une valeur logique en valeur analogique (avec les Presets) afin de faire des opérations mathématiques qui remplaceront les opérateurs ET / OU. | L’astuce consiste à transformer une valeur logique en valeur analogique (avec les Presets) afin de faire des opérations mathématiques qui remplaceront les opérateurs ET / OU. | ||
==Opérateur ET== | L'avantage indéniable par rapport aux fonctionnalités du Moteur de scénario implémenté dans l'IPX800 V5, c'est l'utilisation possible de parenthèses. | ||
L’opérateur ET sera toujours remplacé par une multiplication dans la formule d’un objet fonction. | |||
L'IPX800 fournit des outils que nous pouvons combiner d'innombrables façons pour arriver à un même résultat. | |||
Les méthodes proposées dans cet article pour implémenter la logique combinatoire ne sont pas les seules possibilités. | |||
Vous pouvez trouver d'autres algorithmes ou méthodes, plus proches de vos besoins ou de vos contraintes. | |||
Nous utiliserons des variables dans la formule des objets de type "''Fonction''". | |||
Pour plus d'informations sur cet usage, veuillez vous reporter à cet article : [[Utilisation des variables]] | |||
Tous les diagrammes de cet article sont réalisés avec DRAW.IO, voir mon tutoriel [https://forum.gce-electronics.com/t/draw-io-logiciel-gratuit-pour-schemas-et-diagrammes-interactifs/17442?u=fgtoul ici] | |||
==Opérateur ET (AND)== | |||
=== Table de vérité === | |||
{| class="wikitable" | |||
! colspan="3" |LOI ET | |||
|- | |||
!b\a | |||
!0 | |||
!1 | |||
|- | |||
!0 | |||
|0 | |||
|0 | |||
|- | |||
!1 | |||
|0 | |||
|1 | |||
|} | |||
''a'' ET ''b'' est VRAI si et seulement si ''a'' est VRAI et ''b'' est VRAI | |||
=== Application === | |||
'''L’opérateur ET sera toujours remplacé par une multiplication''' dans la formule d’un objet fonction. | |||
Dans l’exemple ci-dessous, lorsque les 2 conditions sont vraies, l’objet fonction retourne un résultat = 1, ce qui permet de lancer l’action au travers du comparateur. | Dans l’exemple ci-dessous, lorsque les 2 conditions sont vraies, l’objet fonction retourne un résultat = 1, ce qui permet de lancer l’action au travers du comparateur. | ||
| Ligne 23 : | Ligne 61 : | ||
[[Fichier:LOGIQUE COMBINATOIRE ET.jpg|sans_cadre|873x873px]] | [[Fichier:LOGIQUE COMBINATOIRE ET.jpg|sans_cadre|873x873px]] | ||
==Opérateur OU== | ==Opérateur OU (OR, XOR)== | ||
L’opérateur OU est toujours remplacé par une addition. | '''L’opérateur OU est toujours remplacé par une addition'''. | ||
Dans l’exemple précédent, si nous avions voulu une combinaison par OU, nous aurions utilisé l’addition dans la formule de l’objet fonction, le comparateur serait alors A >=1 | Dans l’exemple précédent, si nous avions voulu une combinaison par OU, nous aurions utilisé l’addition dans la formule de l’objet fonction, le comparateur serait alors A >=1 | ||
| Ligne 30 : | Ligne 68 : | ||
En effet, si une des 2 conditions est vraie, le résultat de l’addition est égal à 1. Il serait égal à 2 si les 2 conditions étaient vraies. | En effet, si une des 2 conditions est vraie, le résultat de l’addition est égal à 1. Il serait égal à 2 si les 2 conditions étaient vraies. | ||
Formule de la fonction : ('''$id_preset1$ + $id_preset2$)''' | |||
=== OU inclusif (OR) === | |||
==== Table de vérité ==== | |||
{| class="wikitable" | |||
|+ | |||
! colspan="3" |Loi OU | |||
|- | |||
!b\a | |||
!0 | |||
!1 | |||
|- | |||
!0 | |||
|0 | |||
|1 | |||
|- | |||
!1 | |||
|1 | |||
|1 | |||
|} | |||
''a'' OU ''b'' est VRAI si et seulement si ''a'' est VRAI ou ''b'' est VRAI. | |||
==== Application ==== | |||
[[Fichier:LOGIQUE COMBINATOIRE OU.jpg|sans_cadre|901x901px]] | [[Fichier:LOGIQUE COMBINATOIRE OU.jpg|sans_cadre|901x901px]] | ||
==Combinaisons ET / OU== | L'opérateur A>=B permet de prendre en compte le fait qu'au moins l'une des 2 propositions est vraie. | ||
=== OU exclusif (XOR) === | |||
==== Table de vérité ==== | |||
{| class="wikitable" | |||
|+ | |||
! colspan="3" |Loi OU Exclusif | |||
|- | |||
!b\a | |||
!0 | |||
!1 | |||
|- | |||
!0 | |||
|0 | |||
|1 | |||
|- | |||
!1 | |||
|1 | |||
|0 | |||
|} | |||
''a'' ⊕ ''b'' est VRAI si et seulement si <u>une seule</u> entrée est vraie. | |||
==== Application ==== | |||
Si nous souhaitons qu'une seule des 2 propositions soit vraie pour exécuter l'action, il faut modifier l'opérateur du comparateur. | |||
Avec A==B, la sortie du comparateur sera activée si et seulement si le résultat de la fonction est égal à 1, cela signifie qu''''une seule condition peut être vraie à la fois'''. | |||
[[Fichier:LOGIQUE COMBINATOIRE OU EXCL.jpg|sans_cadre|889x889px]] | |||
==Opérateur NON (NOT)== | |||
==== Table de vérité ==== | |||
{| class="wikitable" | |||
! colspan="2" |Loi NON | |||
|- | |||
!a | |||
!NON a | |||
|- | |||
!0 | |||
|1 | |||
|- | |||
!1 | |||
|0 | |||
|} | |||
La négation de ''a'' est VRAIE si et seulement si ''a'' est FAUX. | |||
==== Application ==== | |||
Pour créer une condition logique avec un capteur NF par exemple, il existe la Tuile <code>'''NON'''</code> dans le Rule Engine. Nous allons voir comment faire dans notre logique. | |||
Pour ce cas, reprenons l’exemple 1 avec A ET B. | |||
Cette fois, nous voulons exécuter une action lorsque '''NON A ET B''' est vraie. | |||
L'ipx800 propose des liens de type "'''NOT'''". Ceux-ci permettent d'inverser la valeur de la ressource avant de l'injecter dans l'IO de destination. | |||
Formule de la fonction : ('''$id_preset1$ * $id_preset2$)''' | |||
''Lorsque la condition A sera ON, le preset 1 recevra OFF sur son entrée "ON/OFF". La sortie sera valorisée à 0.'' | |||
''Lorsque la condition A sera OFF, le preset 1 recevra ON sur son entrée "ON/OFF". La sortie sera valorisée à 1.'' | |||
[[Fichier:LOGIQUE COMBINATOIRE ET NON bis.jpg|sans_cadre|869x869px]] | |||
Une deuxième méthode consiste à inverser les valeurs renseignées dans le Preset1 correspondant à la condition A. | |||
''Lorsque la condition A sera ON, le preset 1 recevra ON sur son entrée "ON/OFF". La sortie sera valorisée à 0.'' | |||
''Lorsque la condition A sera OFF, le preset 1 recevra OFF sur son entrée "ON/OFF". La sortie sera valorisée à 1.'' | |||
[[Fichier:LOGIQUE COMBINATOIRE ET NON.jpg|sans_cadre|871x871px]] | |||
== Opérateur NON-OU (NOR) == | |||
=== Table de vérité === | |||
{| class="wikitable" | |||
! colspan="3" |Loi NON-OU | |||
|- | |||
!b\a | |||
!0 | |||
!1 | |||
|- | |||
!0 | |||
|1 | |||
|0 | |||
|- | |||
!1 | |||
|0 | |||
|0 | |||
|} | |||
NON-OU est vraie si toutes les entrées sont fausses | |||
=== Application === | |||
Nous voulons exécuter l'action seulement si '''ni A ni B sont vraies'''. | |||
Prenons comme précédemment 2 conditions A et B. | |||
D'après les lois de De Morgan, NON (A OU B) est équivalent à '''NON(A) ET NON(B)''' | |||
Réglons le preset1 de manière à ce que la sortie prenne la valeur 1 lorsque A est fausse, faisons de même avec le preset2 pour la condition B. | |||
Vous remarquerez la multiplication dans la formule de la fonction : '''$id_preset1$ * $id_preset2$''' | |||
[[Fichier:LOGIQUE COMBINATOIRE NON-OU.jpg|sans_cadre|814x814px]] | |||
L'autre manière de faire est d'utiliser des Liens de type "NOT" plutôt que d'inverser les valeurs des Presets : | |||
[[Fichier:LOGIQUE COMBINATOIRE NON-OU bis.jpg|sans_cadre|841x841px]] | |||
== Opérateur NON-ET (NAND) == | |||
=== Table de vérité === | |||
{| class="wikitable" | |||
! colspan="3" |Loi NON-ET | |||
|- | |||
!b/a | |||
!0 | |||
!1 | |||
|- | |||
!0 | |||
|1 | |||
|1 | |||
|- | |||
!1 | |||
|1 | |||
|0 | |||
|} | |||
NON-ET est vraie si au moins une entrée est fausse | |||
=== Application === | |||
Nous voulons exécuter l'action seulement si '''au moins une des conditions est fausse'''. | |||
Prenons comme précédemment 2 conditions A et B. | |||
D'après les lois de De Morgan, NON (A ET B) est équivalent à '''NON(A) OU NON(B)''' | |||
Créons des liens de type "NOT" entre la condition et l'entrée du preset respectif. | |||
Réglons le preset1 de manière à ce que la sortie prenne la valeur 1 lorsque A est vraie, faisons de même avec le preset2 pour la condition B. | |||
Vous remarquerez l'addition dans la formule de la fonction. La sortie du comparateur sera activée lorsque l'une des conditions sera fausse. | |||
Formule de la fonction : ('''$id_preset1$ + $id_preset2$)''' | |||
[[Fichier:LOGIQUE COMBINATOIRE NON-ET.jpg|sans_cadre|892x892px]] | |||
== L'équivalence (EQV) == | |||
L'équivalence est une fonction logique qui permet de déterminer si tous les opérandes sont de même valeur. | |||
=== Table de vérité === | |||
{| class="wikitable" | |||
! colspan="3" |EQV | |||
|- | |||
!b/a | |||
!0 | |||
!1 | |||
|- | |||
!0 | |||
|1 | |||
|0 | |||
|- | |||
!1 | |||
|0 | |||
|1 | |||
|} | |||
A EQV B est vrai si A=B | |||
A EQV B <=> '''((A ET B) OU (NON A ET NON B))''' | |||
=== Application : === | |||
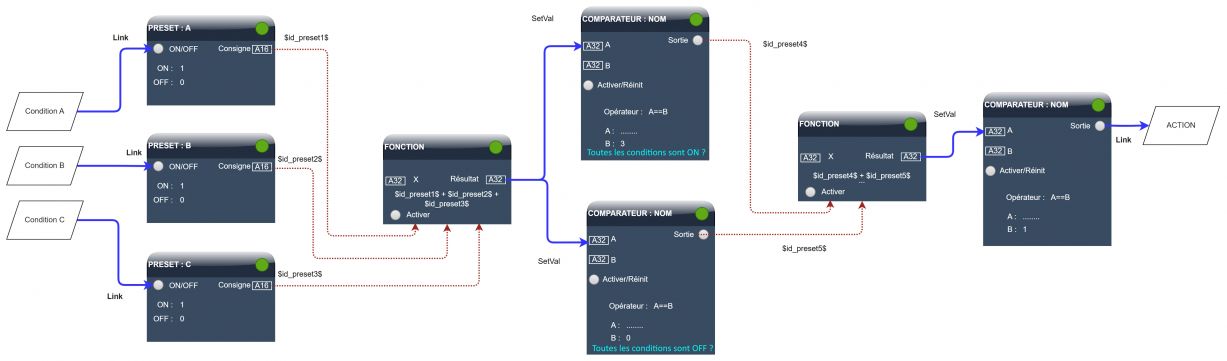
Lorsqu'il n'y a que 2 propositions, la combinaison ET/OU/NON est réalisable sur l'ipx800 v5, mais lorsque le nombre d'opérandes augmente, il vaut mieux appliquer une autre méthode. | |||
Nous compterons donc les opérandes ayant la même valeur. | |||
[[Fichier:EQV complet.jpg|sans_cadre|1227x1227px]] | |||
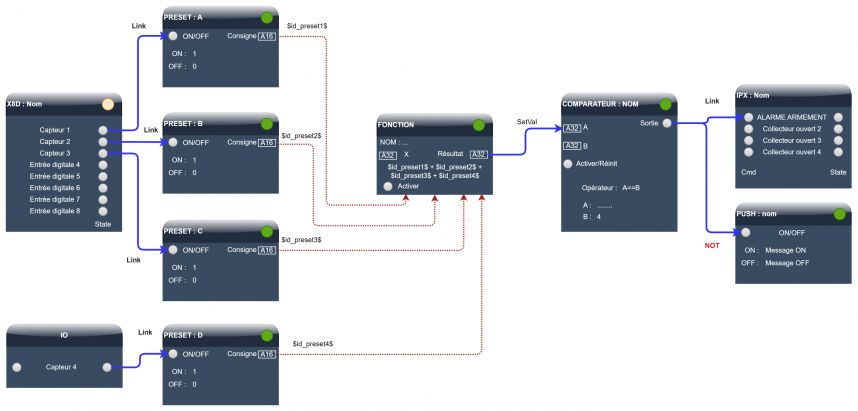
=== Exemple à 4 conditions === | |||
Comportement recherché :Si tous les capteurs NF d'ouverture de la maison sont à l'état ON, l'alarme peut alors être mise en surveillance. | |||
Si au moins un capteur est à l'état OFF, l'utilisateur de l'alarme est invité à vérifier les ouvertures (portes et fenêtres). | |||
Mise en oeuvre : | |||
La méthode consiste à dénombrer seulement les capteurs qui sont à l'état ON. | |||
Si tous les capteurs sont ON, alors le résultat de la fonction est égal à 4, soit le nombre total de capteurs, toutes les conditions sont alors remplies pour l'armement de l'alarme. | |||
Si au moins un capteur est à l'état OFF, la sortie du comparateur se désactive, ce qui a pour effet d'envoyer une notification. | |||
[[Fichier:Exemple EQV.jpg|sans_cadre|858x858px]] | |||
'''<u>Remarque :</u>''' | |||
Pour vérifier si tous les capteurs sont à l'état OFF, il suffit de lier le résultat de la fonction à un comparateur sur lequel l'entrée B est à 0. | |||
=== Détournement de la méthode === | |||
Nous pouvons utiliser la même méthode pour exécuter une action si un certain nombre de conditions est atteint. | |||
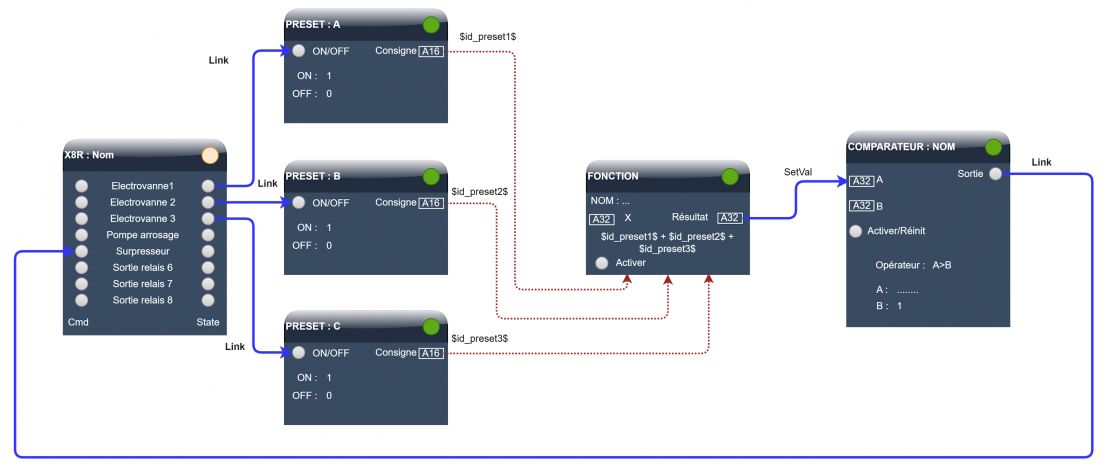
==== Exemple : ==== | |||
Un système d'arrosage automatique comporte 3 voies avec des buses à grand débit. La pompe installée au fond du forage garantit la bonne pression sur une seule voie. | |||
Il faut donc mettre un surpresseur en marche dès que l'on ouvre plus d'une voie. | |||
[[Fichier:Exemple xor.jpg|sans_cadre|1109x1109px]] | |||
== Combinaisons ET / OU == | |||
Le fait d’utiliser la multiplication pour ET et l’addition pour OU dans les formules permet de créer des combinaisons complexes mêlant ET et OU. | Le fait d’utiliser la multiplication pour ET et l’addition pour OU dans les formules permet de créer des combinaisons complexes mêlant ET et OU. | ||
===Exemple avec 3 conditions A, B , C.=== | ===Exemple avec 3 conditions A, B , C.=== | ||
Nous souhaitons exécuter une action lorsque A ET B OU C est | Nous souhaitons exécuter une action lorsque '''A ET B OU C''' est vraie : | ||
[[Fichier:LOGIQUE COMBINATOIRE COMPLEXE.jpg|sans_cadre|905x905px]] | [[Fichier:LOGIQUE COMBINATOIRE COMPLEXE.jpg|sans_cadre|905x905px]] | ||
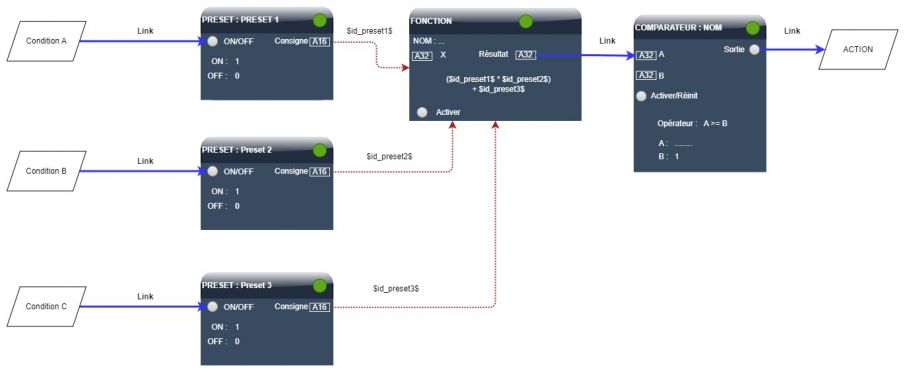
===Exemple avec 4 conditions A, B, C, D=== | ===Exemple avec 4 conditions A, B, C, D=== | ||
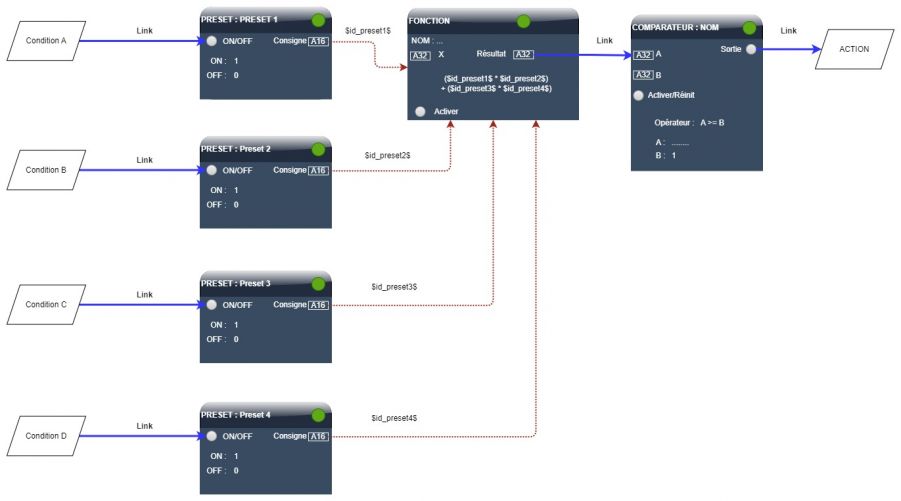
Nous souhaitons exécuter une action lorsque (A ET B) OU (C ET D) est | Nous souhaitons exécuter une action lorsque '''(A ET B) OU (C ET D)''' est vraie. | ||
Formule de la fonction : ('''$id_preset1$ * $id_preset2$) + ($id_preset3$ * $id_preset4$)''' | |||
[[Fichier:LOGIQUE COMBINATOIRE COMPLEXE 2.jpg|sans_cadre|901x901px]] | [[Fichier:LOGIQUE COMBINATOIRE COMPLEXE 2.jpg|sans_cadre|901x901px]] | ||
== | == Exemples pratiques == | ||
=== Exemple 1 === | |||
Nous souhaitons que le spot de la piscine s'allume à la pression d'un bouton poussoir dans une certaine plage horaire. | |||
* Condition A : l'entrée digitale 1 liée au bouton poussoir passe à l'état ON | |||
* Condition B : la plage horaire est propice, la sortie du calendrier est activée. | |||
* L'action consiste à démarrer la temporisation d'éclairage lorsque les 2 conditions sont vraies. | |||
[[Fichier:LOGIQUE COMBINATOIRE ET | |||
Il faut donc que l'expression '''CONDITION A ET CONDITION B''' soit vraie pour que l'action soit exécutée | |||
[[Fichier:LOGIQUE COMBINATOIRE EXEMPLE1.jpg|sans_cadre|1185x1185px]] | |||
=== Exemple 2 === | |||
Un capteur de mouvements 12 V est connecté à une X-8D. Il émet une impulsion de 5 millisecondes lors d'une détection. | |||
Nous souhaitons que le luminaire soit allumé pendant 60 secondes à condition que la luminosité soit inférieure ou égale à 6 LUX. | |||
* Condition A : l'entrée digitale 1 liée au capteur passe à l'état ON | |||
* Condition B : la luminosité est inférieure à 6 LUX, la sortie du comparateur est activée. | |||
* L'action consiste à démarrer la temporisation d'éclairage lorsque les 2 conditions sont vraies. | |||
[[Fichier:LOGIQUE COMBINATOIRE EX2.jpg|sans_cadre|1279x1279px]] | |||
== Astuce == | |||
[[Fichier:Image io-preset.png|sans_cadre|600x600px]] | |||
Une IO à l'état ON vaut 1 et vaut 0 à l'état OFF. | |||
Dans le cas ci-dessus, la sortie du Preset a donc la même valeur que l'IO elle-même. | |||
Le Preset est indispensable dans le cas où vous souhaitez lier cette IO à l'entrée analogique d'un autre objet et pour la compréhension globale du Wiki, j'ai utilisé systématiquement un objet Preset. | |||
Cependant, au lieu d'utiliser la sortie analogique du preset sous forme de variable dans une fonction par exemple, vous pouvez inclure l'ID de cette IO directement dans la formule. | |||
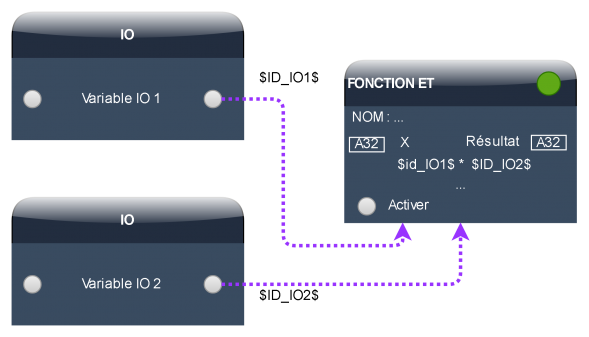
Exemple avec la reprise de la fonction ET : | |||
[[Fichier:Image IO-Preset-sample.png|sans_cadre|589x589px]] | |||
Le résultat de la fonction sera 1 si les 2 IO sont ON, et 0 si au moins l'une des 2 est OFF. | |||
== Matrice outil == | |||
=== La Matrice === | |||
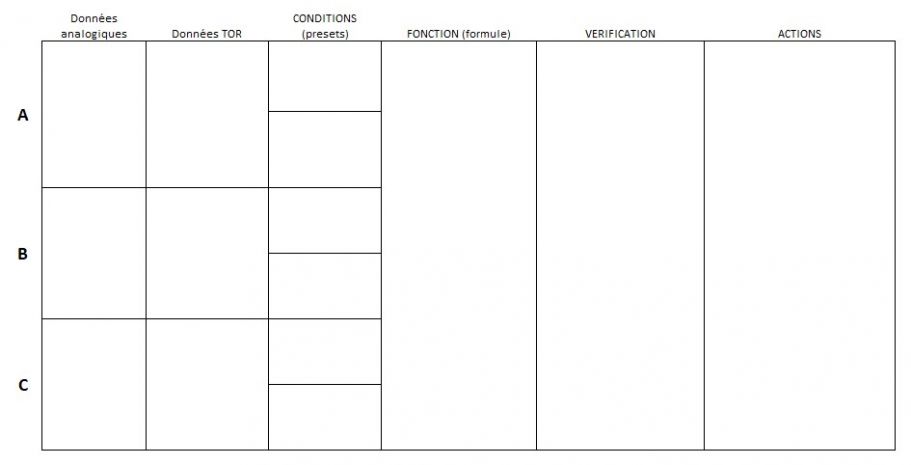
Vous avez pu constater que la construction des liens dans cet article suit toujours une même structure, qui pourrait être mise en tableau | |||
[[Fichier:Matrice outil.jpg|sans_cadre|911x911px]] | |||
Cette structure peut aider à construire vos liens et objets. | |||
=== Exemples d'utilisation === | |||
==== Reprise de l'exemple 1. ==== | |||
Rappel : | |||
Nous souhaitons que le spot de la piscine s'allume à la pression d'un bouton poussoir dans une certaine plage horaire. | |||
[[Fichier:Logique Combinatoire Matrice exemple 1.jpg|sans_cadre|933x933px]] | |||
==== Reprise de l'exemple 2. ==== | |||
Rappel : | |||
Un capteur de mouvements 12 V est connecté à une X-8D. Il émet une impulsion de 5 millisecondes lors d'une détection. | |||
Nous souhaitons que le luminaire soit allumé pendant 60 secondes à condition que la luminosité soit inférieure ou égale à 6 LUX. | |||
[[Fichier:Matrice exemple 2b.jpg|sans_cadre|902x902px]] | |||
Version actuelle datée du 5 décembre 2023 à 15:14
Introduction
| |||
|---|---|---|---|

| |||
| Nom | Logique combinatoire | ||
| Famille | IPX800 V5 | ||
| Wiki créé le | 22/10/2023 | ||
| Wiki mis à jour le | 28/10/2023 | ||
| Auteur | @fgtoul | ||
Le moteur de scénario de l'ipx800 V5 permet de créer des combinaisons logiques grâce aux opérateurs ET, OU, NON.
Nous pouvons tout à fait créer ce même type de condition complexe en utilisant des liens seulement.
L’astuce consiste à transformer une valeur logique en valeur analogique (avec les Presets) afin de faire des opérations mathématiques qui remplaceront les opérateurs ET / OU.
L'avantage indéniable par rapport aux fonctionnalités du Moteur de scénario implémenté dans l'IPX800 V5, c'est l'utilisation possible de parenthèses.
L'IPX800 fournit des outils que nous pouvons combiner d'innombrables façons pour arriver à un même résultat.
Les méthodes proposées dans cet article pour implémenter la logique combinatoire ne sont pas les seules possibilités.
Vous pouvez trouver d'autres algorithmes ou méthodes, plus proches de vos besoins ou de vos contraintes.
Nous utiliserons des variables dans la formule des objets de type "Fonction".
Pour plus d'informations sur cet usage, veuillez vous reporter à cet article : Utilisation des variables
Tous les diagrammes de cet article sont réalisés avec DRAW.IO, voir mon tutoriel ici
Opérateur ET (AND)
Table de vérité
| LOI ET | ||
|---|---|---|
| b\a | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
a ET b est VRAI si et seulement si a est VRAI et b est VRAI
Application
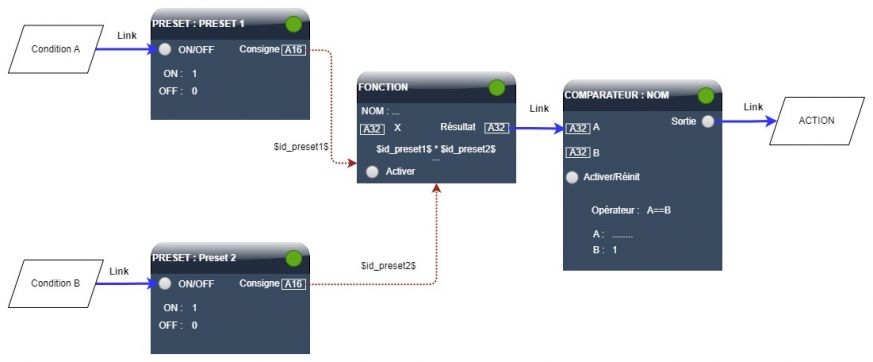
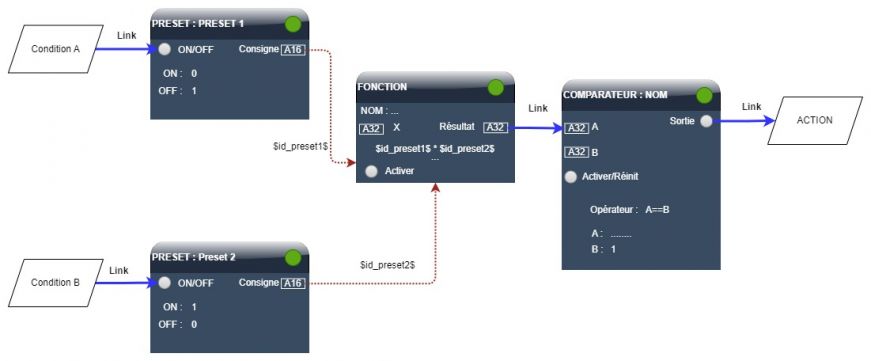
L’opérateur ET sera toujours remplacé par une multiplication dans la formule d’un objet fonction.
Dans l’exemple ci-dessous, lorsque les 2 conditions sont vraies, l’objet fonction retourne un résultat = 1, ce qui permet de lancer l’action au travers du comparateur.
Opérateur OU (OR, XOR)
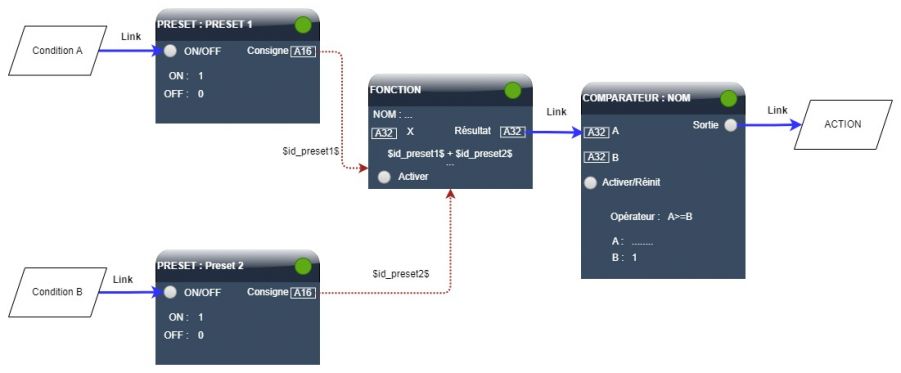
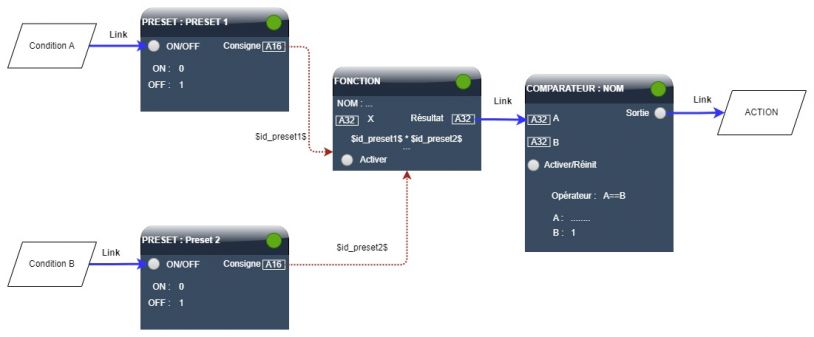
L’opérateur OU est toujours remplacé par une addition.
Dans l’exemple précédent, si nous avions voulu une combinaison par OU, nous aurions utilisé l’addition dans la formule de l’objet fonction, le comparateur serait alors A >=1
En effet, si une des 2 conditions est vraie, le résultat de l’addition est égal à 1. Il serait égal à 2 si les 2 conditions étaient vraies.
Formule de la fonction : ($id_preset1$ + $id_preset2$)
OU inclusif (OR)
Table de vérité
| Loi OU | ||
|---|---|---|
| b\a | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
a OU b est VRAI si et seulement si a est VRAI ou b est VRAI.
Application
L'opérateur A>=B permet de prendre en compte le fait qu'au moins l'une des 2 propositions est vraie.
OU exclusif (XOR)
Table de vérité
| Loi OU Exclusif | ||
|---|---|---|
| b\a | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
a ⊕ b est VRAI si et seulement si une seule entrée est vraie.
Application
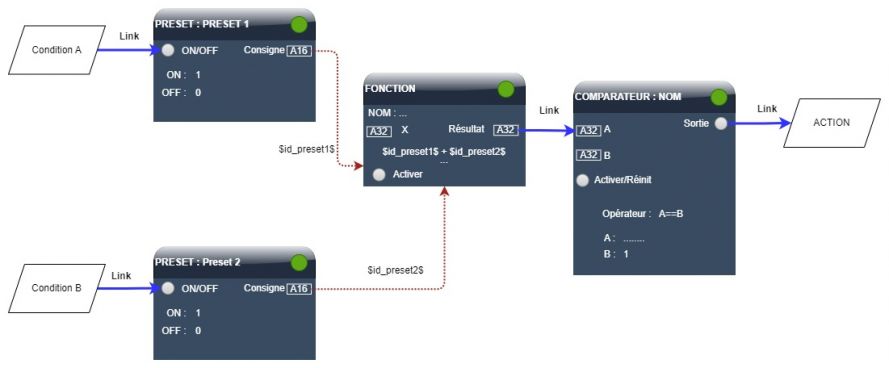
Si nous souhaitons qu'une seule des 2 propositions soit vraie pour exécuter l'action, il faut modifier l'opérateur du comparateur.
Avec A==B, la sortie du comparateur sera activée si et seulement si le résultat de la fonction est égal à 1, cela signifie qu'une seule condition peut être vraie à la fois.
Opérateur NON (NOT)
Table de vérité
| Loi NON | |
|---|---|
| a | NON a |
| 0 | 1 |
| 1 | 0 |
La négation de a est VRAIE si et seulement si a est FAUX.
Application
Pour créer une condition logique avec un capteur NF par exemple, il existe la Tuile NON dans le Rule Engine. Nous allons voir comment faire dans notre logique.
Pour ce cas, reprenons l’exemple 1 avec A ET B.
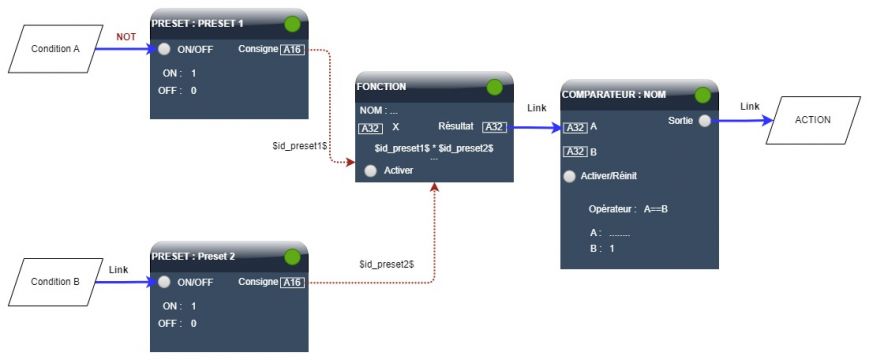
Cette fois, nous voulons exécuter une action lorsque NON A ET B est vraie.
L'ipx800 propose des liens de type "NOT". Ceux-ci permettent d'inverser la valeur de la ressource avant de l'injecter dans l'IO de destination.
Formule de la fonction : ($id_preset1$ * $id_preset2$)
Lorsque la condition A sera ON, le preset 1 recevra OFF sur son entrée "ON/OFF". La sortie sera valorisée à 0. Lorsque la condition A sera OFF, le preset 1 recevra ON sur son entrée "ON/OFF". La sortie sera valorisée à 1.
Une deuxième méthode consiste à inverser les valeurs renseignées dans le Preset1 correspondant à la condition A.
Lorsque la condition A sera ON, le preset 1 recevra ON sur son entrée "ON/OFF". La sortie sera valorisée à 0. Lorsque la condition A sera OFF, le preset 1 recevra OFF sur son entrée "ON/OFF". La sortie sera valorisée à 1.
Opérateur NON-OU (NOR)
Table de vérité
| Loi NON-OU | ||
|---|---|---|
| b\a | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
NON-OU est vraie si toutes les entrées sont fausses
Application
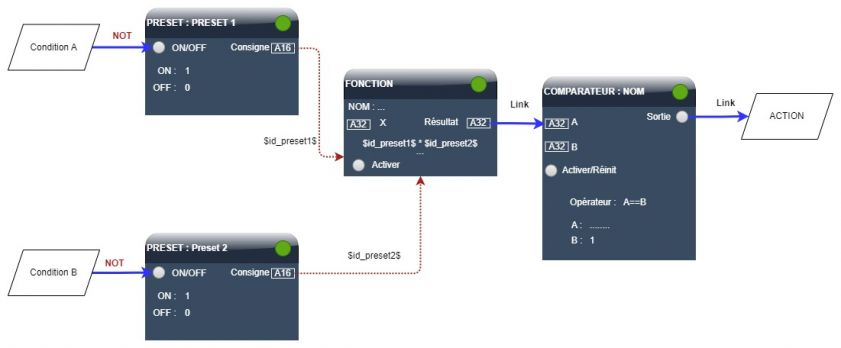
Nous voulons exécuter l'action seulement si ni A ni B sont vraies.
Prenons comme précédemment 2 conditions A et B.
D'après les lois de De Morgan, NON (A OU B) est équivalent à NON(A) ET NON(B)
Réglons le preset1 de manière à ce que la sortie prenne la valeur 1 lorsque A est fausse, faisons de même avec le preset2 pour la condition B.
Vous remarquerez la multiplication dans la formule de la fonction : $id_preset1$ * $id_preset2$
L'autre manière de faire est d'utiliser des Liens de type "NOT" plutôt que d'inverser les valeurs des Presets :
Opérateur NON-ET (NAND)
Table de vérité
| Loi NON-ET | ||
|---|---|---|
| b/a | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
NON-ET est vraie si au moins une entrée est fausse
Application
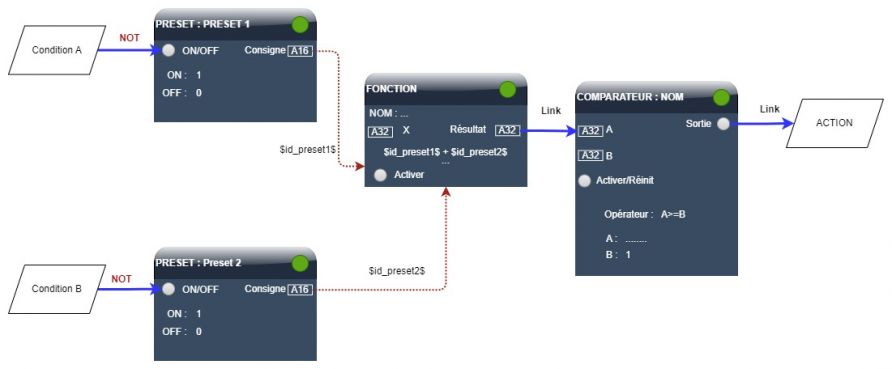
Nous voulons exécuter l'action seulement si au moins une des conditions est fausse.
Prenons comme précédemment 2 conditions A et B.
D'après les lois de De Morgan, NON (A ET B) est équivalent à NON(A) OU NON(B)
Créons des liens de type "NOT" entre la condition et l'entrée du preset respectif.
Réglons le preset1 de manière à ce que la sortie prenne la valeur 1 lorsque A est vraie, faisons de même avec le preset2 pour la condition B.
Vous remarquerez l'addition dans la formule de la fonction. La sortie du comparateur sera activée lorsque l'une des conditions sera fausse.
Formule de la fonction : ($id_preset1$ + $id_preset2$)
L'équivalence (EQV)
L'équivalence est une fonction logique qui permet de déterminer si tous les opérandes sont de même valeur.
Table de vérité
| EQV | ||
|---|---|---|
| b/a | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
A EQV B est vrai si A=B
A EQV B <=> ((A ET B) OU (NON A ET NON B))
Application :
Lorsqu'il n'y a que 2 propositions, la combinaison ET/OU/NON est réalisable sur l'ipx800 v5, mais lorsque le nombre d'opérandes augmente, il vaut mieux appliquer une autre méthode.
Nous compterons donc les opérandes ayant la même valeur.
Exemple à 4 conditions
Comportement recherché :Si tous les capteurs NF d'ouverture de la maison sont à l'état ON, l'alarme peut alors être mise en surveillance.
Si au moins un capteur est à l'état OFF, l'utilisateur de l'alarme est invité à vérifier les ouvertures (portes et fenêtres).
Mise en oeuvre :
La méthode consiste à dénombrer seulement les capteurs qui sont à l'état ON.
Si tous les capteurs sont ON, alors le résultat de la fonction est égal à 4, soit le nombre total de capteurs, toutes les conditions sont alors remplies pour l'armement de l'alarme.
Si au moins un capteur est à l'état OFF, la sortie du comparateur se désactive, ce qui a pour effet d'envoyer une notification.
Remarque :
Pour vérifier si tous les capteurs sont à l'état OFF, il suffit de lier le résultat de la fonction à un comparateur sur lequel l'entrée B est à 0.
Détournement de la méthode
Nous pouvons utiliser la même méthode pour exécuter une action si un certain nombre de conditions est atteint.
Exemple :
Un système d'arrosage automatique comporte 3 voies avec des buses à grand débit. La pompe installée au fond du forage garantit la bonne pression sur une seule voie.
Il faut donc mettre un surpresseur en marche dès que l'on ouvre plus d'une voie.
Combinaisons ET / OU
Le fait d’utiliser la multiplication pour ET et l’addition pour OU dans les formules permet de créer des combinaisons complexes mêlant ET et OU.
Exemple avec 3 conditions A, B , C.
Nous souhaitons exécuter une action lorsque A ET B OU C est vraie :
Exemple avec 4 conditions A, B, C, D
Nous souhaitons exécuter une action lorsque (A ET B) OU (C ET D) est vraie.
Formule de la fonction : ($id_preset1$ * $id_preset2$) + ($id_preset3$ * $id_preset4$)
Exemples pratiques
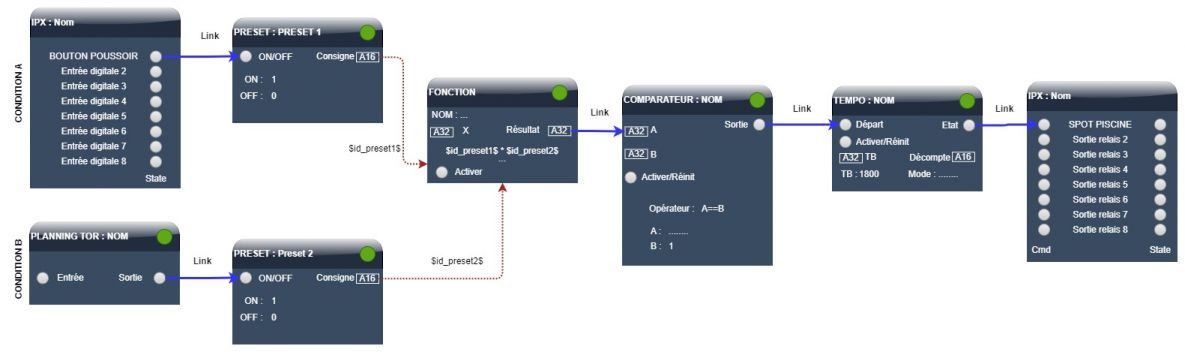
Exemple 1
Nous souhaitons que le spot de la piscine s'allume à la pression d'un bouton poussoir dans une certaine plage horaire.
- Condition A : l'entrée digitale 1 liée au bouton poussoir passe à l'état ON
- Condition B : la plage horaire est propice, la sortie du calendrier est activée.
- L'action consiste à démarrer la temporisation d'éclairage lorsque les 2 conditions sont vraies.
Il faut donc que l'expression CONDITION A ET CONDITION B soit vraie pour que l'action soit exécutée
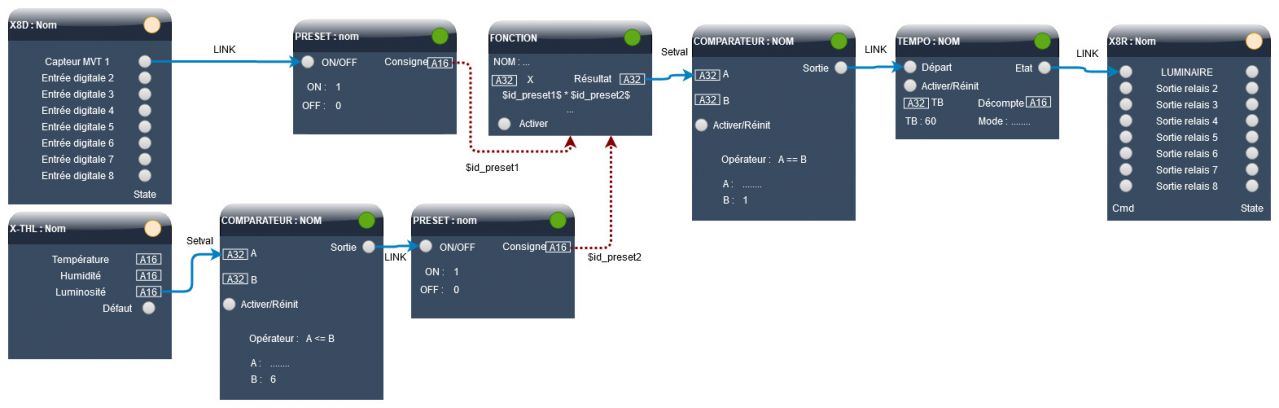
Exemple 2
Un capteur de mouvements 12 V est connecté à une X-8D. Il émet une impulsion de 5 millisecondes lors d'une détection.
Nous souhaitons que le luminaire soit allumé pendant 60 secondes à condition que la luminosité soit inférieure ou égale à 6 LUX.
- Condition A : l'entrée digitale 1 liée au capteur passe à l'état ON
- Condition B : la luminosité est inférieure à 6 LUX, la sortie du comparateur est activée.
- L'action consiste à démarrer la temporisation d'éclairage lorsque les 2 conditions sont vraies.
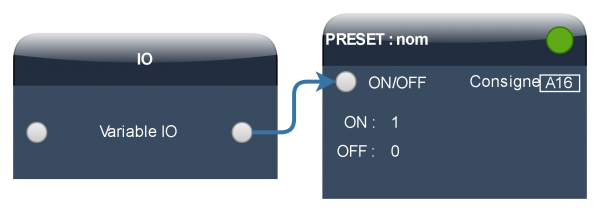
Astuce
Une IO à l'état ON vaut 1 et vaut 0 à l'état OFF.
Dans le cas ci-dessus, la sortie du Preset a donc la même valeur que l'IO elle-même.
Le Preset est indispensable dans le cas où vous souhaitez lier cette IO à l'entrée analogique d'un autre objet et pour la compréhension globale du Wiki, j'ai utilisé systématiquement un objet Preset.
Cependant, au lieu d'utiliser la sortie analogique du preset sous forme de variable dans une fonction par exemple, vous pouvez inclure l'ID de cette IO directement dans la formule.
Exemple avec la reprise de la fonction ET :
Le résultat de la fonction sera 1 si les 2 IO sont ON, et 0 si au moins l'une des 2 est OFF.
Matrice outil
La Matrice
Vous avez pu constater que la construction des liens dans cet article suit toujours une même structure, qui pourrait être mise en tableau
Cette structure peut aider à construire vos liens et objets.
Exemples d'utilisation
Reprise de l'exemple 1.
Rappel : Nous souhaitons que le spot de la piscine s'allume à la pression d'un bouton poussoir dans une certaine plage horaire.
Reprise de l'exemple 2.
Rappel : Un capteur de mouvements 12 V est connecté à une X-8D. Il émet une impulsion de 5 millisecondes lors d'une détection. Nous souhaitons que le luminaire soit allumé pendant 60 secondes à condition que la luminosité soit inférieure ou égale à 6 LUX.