Les entrées analogiques sur IPX800 V4

Les Entrées analogiques de l’IPX800 V4

Les entrées analogiques de l’IPX800 permettent de mesurer des tensions, allant de 0V à 3.3V maximum. Il convient de connecter le capteur entre le GND et 3.3V. Le fil correspondant à la mesure sera connecté à l’entrée analogique cas des capteurs TC-100 ; TC4012 ; SHT-X3 vendus par GCE)

300px

Si des tensions supérieures à 3.3 V doivent être mesurées, alors il faudra utiliser un pont diviseur afin de ramener cette tension à 3.3v maximum. Si le capteur nécessite une alimentation plus élevée, ne pas lui raccorder le 3.3V.

A. Le Convertisseur Analogique vers Numérique (CAN en français, ADC en anglais)

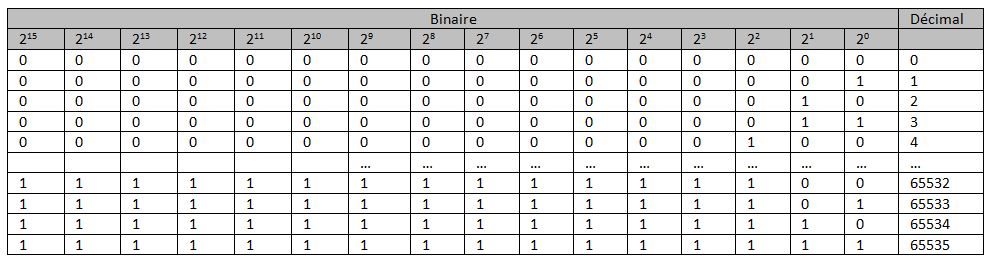
Chaque entrée analogique de l’IPX constitue un CAN, capable de traduire une tension (de 0 à 3.3 V) en une grandeur numérique codée sur 16 bits (Résolution) pour la V4.

Chaque bit peut prendre 2 valeurs (0 ou 1). Nous obtenons alors 2^16 combinaisons différentes, soit 65536 valeurs possibles (de 0 à 65535 inclus).

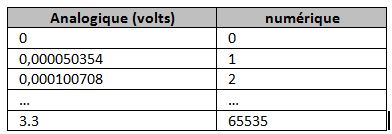
Pour une valeur analogique 0 V, l’IPX800 retourne une valeur numérique 0. Pour une tension pleine échelle 3.3 V (le maximum) , l’IPX800 V4 retourne 65535. Entre chaque point de mesure, il y a donc 3.3/65535 = 0,000050354 V

Donc, pour chaque grandeur analogique (tension de 0 à 3.3v), le convertisseur renvoie une valeur de 0 à 65535, représentant le multiple de 0,000050354 V le plus proche de la valeur mesurée. Pour retrouver la valeur analogique mesurée, il suffit alors de calculer le produit entre la valeur numérique fournie par l’IPX et 0,000050354. Nous avons là une fonction « voltmètre ». Exemple : l’IPX800 V4 renvoie une valeur brute de 619. 619 * 0,000050354 = 0.031169126 La tension appliquée à l’entrée analogique est donc de 0.03 V

B. Application : un anémomètre analogique

Soit un anémomètre avec les caractéristiques suivantes : Sortie : 0.4V à 2V La tension va varier de 0,4V (Vent à 0m/s) à 2V ( vent à 32,4m/s). Nous n’utilisons donc pas la totalité de la plage possible de lectures de l’IPX qui peut aller jusqu’à 3.3v. - Pour une lecture de 2V, nous aurons donc une valeur numérique de 2 / 0,000050354 = 39719. 39719 sera donc la valeur numérique maxi calculée par l’IPX pour 32.4 m/s - Pour une lecture de 0.4v nous aurons une valeur numérique de 0.4 / 0,000050354 = 7944 7944 sera la valeur minimale calculée par l’IPX800.

Nous avons donc 39719 - 7944 = 31775 valeurs numériques utilisables par l’IPX800 correspondant à une plage [0.4 V ; 2 V].

Voyons cela sur un graphique

Avec le graphique nous voyons que l’IPX peut faire correspondre 31775 valeurs proportionnelles à la tension de sortie de notre capteur.

Cela revient donc à dire que l’IPX peut faire correspondre 31775 valeurs proportionnelles à la vitesse du vent, dans la plage [0 ; 32.4] m/s

Chaque valeur numérique retournée est donc un multiple de 32,4 / 31775=0,001019669 m/s De là, nous déduisons la formule (avec prise en compte de l’origine à 7944)

Soit A la valeur analogique recherchée, et D la valeur renvoyée par l’IPX. Nous avons déterminé que A = (D - 7944) * 0,001019669 Dans l’IPX800, nous écrirons la formule sous la forme décimal vers analog : (x - 7944) * 0,001019669

Inversement Soit A la valeur analogique recherchée, et D la valeur renvoyée par l’IPX. Nous savons que A = (D - 7944) * 0,001019669 <=> A / 0.001019669= D -7944 <=> D = (A / 0.001019669) + 7944

Dans l’IPX800, nous écrirons la formule sous la forme analog vers décimal : (x / 0,001019669) + 7944

Pour vérifier la formule, prenons la valeur 39719 calculée ci-dessus,

elle retourne bien (39719 - 7944)* 0,001019669 = 32.4

C. Pour mesurer une tension supérieure à 3.3 V

1. Principe

La tension applicable sur une entrée analogique de l’IPX800 doit impérativement être inférieure à 3.3v. Au dessus, elle ne sera pas mesurée et vous risquez d’endommager l’IPX. Si vous devez mesurer une tension plus grande, il faut utiliser un pont diviseur de tension. Le but n’est pas ici d’expliquer le fonctionnement d’un diviseur de tension, mais de voir son application à l’IPX800. Nous savons que l’impédance interne de l’entrée analogique de l’IPX800 est de 4700 Ω

Aux bornes de l’entrée analogique, la tension Vs est telle que Vs = (R1/(R1+R2)) x Ve

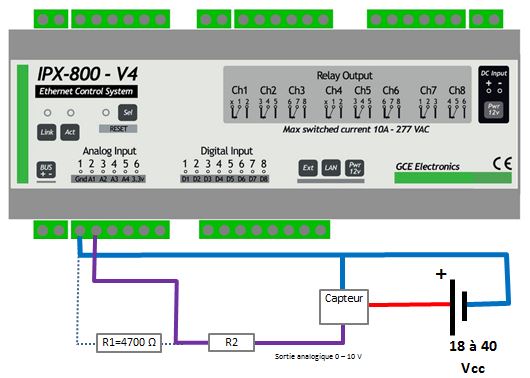
2. Exemple d’un capteur analogique avec sortie 0 – 10v

      La résistance R1 est interne à l’IPX800. Elle est représentée ici pour la compréhension du schéma. Ne pas la câbler.
      Adaptez les branchements en fonction des recommandations constructeur.

Vs = (R1/(R1+R2)) x Ve

Isolons le terme R2 :

R2 = R1 x (Ve / Vs) - R1

Remplaçons par les valeurs numériques.

Nous ajouterons 10% de marge à notre tension d’entrée par mesure de sécurité (soit 11V au lieu de 10V) :

R2 = 4700 x ((11 / 3.3) – 4700

R2 = 10966 Ω

Il conviendra de prendre une résistance de 11 kΩ. (valeur standard supérieure la plus proche)

Recalculons la tension max aux bornes de l’IPX

Vs = (R1/(R1+R2)) x Ve

Vs=(4.7 / (4.7 + 11)) * 10 <=> Vs=3.0 V

Pour 10 V en sortie du capteur, l’IPX800 ne « verra » donc que 3.0 V aux bornes de son entrée analogique.

nous devons nous assurer que notre résistance peut supporter le courant qui circulera

Ve=I * (R1 +R2)

<=> I=Ve/(R1+R2)

<=> I=10 / (11000 +4700) = 0.00063 A

P=Ve.I <=> P=10 x 0.00063 A <=> P=0.007 W => Une résistance 1/4W suffira.

D. Utilisation de capteurs analogiques avec sortie en courant

Le courant de sortie est fonction linéaire de la gamme de mesure.

Exemple : variation de 0 à 20 mA pour une mesure de 0 à 40°C.

Nous pouvons les rencontrer sous différents formats : • 0-20 mA : fréquent • 4-20 mA : le plus répandu ; permet de détecter les ruptures de conducteur ou les défauts de mesure (si I < 4mA) • 0-10mA : rare • 0-16mA : rare Les avantages de ces capteurs : • Pas de perte de signal sur une longue distance. Le courant est constant sur toute la longueur de la boucle • Peu sensible aux interférences électromagnétiques

Utilisation des capteurs 0-20 mA ou 4-20 mA Pour utiliser ce type de capteur, il suffit d’ajouter une résistance de 165 Ω aux bornes de la sortie du capteur. Avec la loi d’Ohm, nous prévoyons en effet que lorsque la sortie délivrera 20mA (son maximum), la tension aux bornes de la résistance sera U=R * I U = 165 * 0.020 U = 3.3 V Nous faisons mesurer cette tension par l’IPX.

   Attention :
   Si le capteur est susceptible d’émettre un courant plus fort (22 mA dans certains cas), utilisez une résistance de 150 Ω
   Il existe des capteurs à 3 ou 4 fils. Adaptez les branchements en fonction des recommandations constructeur.
   

La formule sera calculée en fonction de la tension aux bornes de la résistance. Exemple d’un capteur de température 0 à 40°C en 4-20 mA (voir la méthode plus haut) Avec la loi d’Ohm, à 20 mA, nous savons que nous aurons 3.3V (le CAN traduira par 65535) De même, à 4 mA, nous aurons 0.66 V (le CAN traduira par 13107) La plage de mesure [0 – 40°C] est donc répartie sur 52428 valeurs, soit un pas de 0.0007629

La formule de notre capteur sera donc

   digital vers analog : (x - 13107) * 0.0007629

   analog vers digital : (x / 0.0007629) + 13107

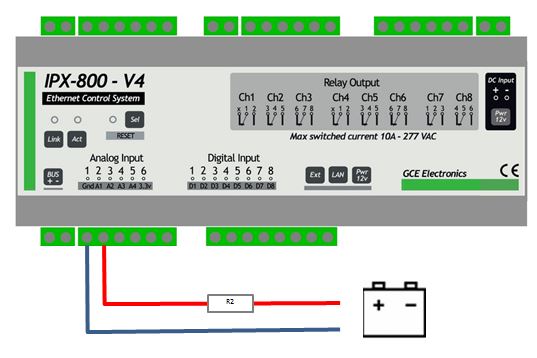
E. Pour mesurer la tension aux bornes d’une batterie

Comme nous l’avons vu plus haut, pour mesurer une tension supérieure à 3.3V, il faut avoir recours à un pont diviseur de tension.

Rien de bien compliqué dans ce cas de figure. La seule chose qui doit susciter votre attention est de bien déterminer la valeur de la résistance en fonction de la tension de charge de la batterie. En effet, il n’est pas rare que des batteries pour automobile ait une tension grimpant jusqu’à 18 V. Si nous ajoutons les 10% de marge, la résistance serait alors à calculer sur 20 V, et non sur 12 V