Différences entre les versions de « Déterminer l'équation d'un Capteur analogique »
(Page créée avec « 'test ») |
|||
| Ligne 1 : | Ligne 1 : | ||
===Préambule=== | |||
j’avais écrit quelques articles afin de vous aider à déterminer l’équation d’une courbe en sortie de capteur. | |||
La méthode consistait à esayer de superposer une parabole à la courbe donnée par le fabricant. L’équation de la parabole était alors calculée en fonction des coordonnées de 3 points relevés sur la courbe fournie. | |||
Si la méthode vous intéresse, vous pouvez suivre le fil à partir d’[https://forum.gce-electronics.com/t/capteur-analogique-non-lineaire/5519/5?u=fgtoul ici] | |||
Cette méthode laissait malgré tout une marge d’erreur plus ou moins confortable, car la courbe d’origine n’était pas forcément parabolique (polynomiale d’ordre 2), elle pouvait être de type linéaire, exponentielle, logarithmique ou autre. Il me fallait trouver une solution plus "universelle". | |||
===But=== | |||
Ce tutoriel va vous permettre d’établir l’équation de votre graphique, grâce à l’ajout d’une courbe de tendance (aussi appelée courbe de régression) , certains fabricants ne donnant pas l’équation pour leur produit. | |||
==Cas pratique== | |||
Pour commencer, prenons l’exemple d’un capteur de distance (télémètre) à infra-rouges (SHARP GP2Y0A02) | |||
[[Fichier:GP2Y0A02.png]] | |||
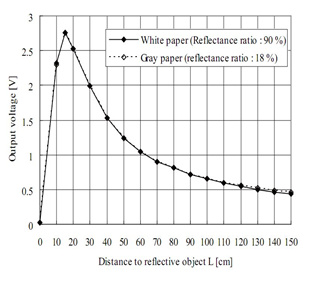
Voici son abaque : | |||
[[Fichier:GP2Y0A02_abaque.png]] | |||
==Méthode== | |||
===1. Le relevé=== | |||
La première étape consiste à faire un relevé des données, de la manière la plus précise possible. Nous nous intéresserons à l’intervalle [20 ; 150] puisque cela correspond à la plage de mesure du capteur. | |||
Pour cela, je conseille d’agrandir le graphique, puis de relever chaque point à la règle en recalculant ses coordonnées grâce à la règle de trois basée sur l’échelle. | |||
Pour la courbe ci-dessus, le relevé donnerait ceci (aux arrondis près): | |||
Distance (cm) Tension (V) | |||
20 2,5 | |||
30 2 | |||
40 1,571428571 | |||
50 1,257142857 | |||
60 1,071428571 | |||
70 0,928571429 | |||
80 0,814285714 | |||
90 0,728571429 | |||
100 0,685714286 | |||
110 0,6 | |||
120 0,557142857 | |||
130 0,528571429 | |||
140 0,5 | |||
150 0,471428571 | |||
Version du 6 novembre 2017 à 11:57
Préambule
j’avais écrit quelques articles afin de vous aider à déterminer l’équation d’une courbe en sortie de capteur. La méthode consistait à esayer de superposer une parabole à la courbe donnée par le fabricant. L’équation de la parabole était alors calculée en fonction des coordonnées de 3 points relevés sur la courbe fournie.
Si la méthode vous intéresse, vous pouvez suivre le fil à partir d’ici
Cette méthode laissait malgré tout une marge d’erreur plus ou moins confortable, car la courbe d’origine n’était pas forcément parabolique (polynomiale d’ordre 2), elle pouvait être de type linéaire, exponentielle, logarithmique ou autre. Il me fallait trouver une solution plus "universelle".
But
Ce tutoriel va vous permettre d’établir l’équation de votre graphique, grâce à l’ajout d’une courbe de tendance (aussi appelée courbe de régression) , certains fabricants ne donnant pas l’équation pour leur produit.
Cas pratique
Pour commencer, prenons l’exemple d’un capteur de distance (télémètre) à infra-rouges (SHARP GP2Y0A02)
Voici son abaque :
Méthode
1. Le relevé
La première étape consiste à faire un relevé des données, de la manière la plus précise possible. Nous nous intéresserons à l’intervalle [20 ; 150] puisque cela correspond à la plage de mesure du capteur. Pour cela, je conseille d’agrandir le graphique, puis de relever chaque point à la règle en recalculant ses coordonnées grâce à la règle de trois basée sur l’échelle.
Pour la courbe ci-dessus, le relevé donnerait ceci (aux arrondis près): Distance (cm) Tension (V) 20 2,5 30 2 40 1,571428571 50 1,257142857 60 1,071428571 70 0,928571429 80 0,814285714 90 0,728571429 100 0,685714286 110 0,6 120 0,557142857 130 0,528571429 140 0,5 150 0,471428571